Estoy haciendo EE hw ahora mismo mientras repaso mis notas, me doy cuenta de que mi profesor dijo que e ^ (j pi / 4) = 1 pero ¿cómo?
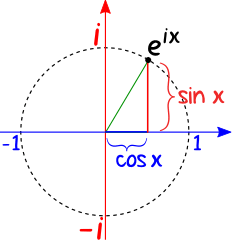
Usando Euler, obtendría e (j pi / 4) = cos (pi / 4) + jsin (pi / 4) = 0.7071 + j0.7071 
relación de Euler (e ^ (j * pi / 4)
-4
pregunta JavaBeginner
2 respuestas
5
No sé cómo logró obtener cos (pi / 4) = 0.5 porque cos (45) = 0.7071 y sin (45) = 0.7071 también. (Estos errores fueron subsecuentemente editados fuera de la pregunta).
Por lo tanto, \ $ \ sqrt {0.7071 ^ 2 + 0.7071 ^ 2} \ $ = 1
respondido por el Andy aka
3
Me gustaría señalar que las exponenciales complejas son otra forma de escribir números complejos. Por lo tanto, si no hay un coeficiente de exp (j * omega), se supone que la magnitud es 1. El coeficiente es la magnitud.
$$ z = \ alpha + j \ beta = r e ^ {j \ omega} $$ $$ | z | = \ sqrt {\ alpha ^ 2 + \ beta ^ 2} = r $$ $$ \ angle z = \ arg (z) = \ omega = \ arctan (\ frac {\ beta} {\ alpha}) $$
Espero que esto ayude
respondido por el
crowie
Lea otras preguntas en las etiquetas laplace-transform z-transform