Cuando construimos circuitos de amplificadores operacionales que usan retroalimentación negativa, como así:
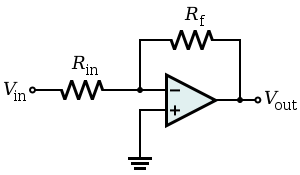
...podemosanalizarelcircuitomuyfácilmente,asumiendoque$$v^-=v^+$$debidoaunaretroalimentaciónnegativa(cuandotambiénsesuponequeelamplificadoroperacionalesideal,porsupuesto).
Ademásdeloscasosobviosdealtaprecisióndondeestosmodelossimplificadossedescomponen,¿cuándoesestoycuándonoesválido?Porejemplo,sireemplazamoslaresistenciaderetroalimentaciónconalgúnotroelemento,talvezuncapacitor,uninductor,undiodo(diododesilicioregular,undiodoZener,etc.),oalgunacombinacióndeellosyotroselementosdecircuitoscomunes,¿cómosabemosdónde?lasimplificaciónesválida?
Además,inclusosinosquedamosconunaresistenciacomoelementoderetroalimentación,yaquelaresistenciasevuelvemuy,muyalta,enalgúnmomentopodemosconsiderarlocomouncircuitoabierto,yclaramenteestemodeloserompeenalgúnpuntodelcamino.
Entonces,lapreguntaes:¿bajoquérestriccionesesestaaproximación"suficientemente cierta" para dar resultados útiles?
EDIT:
Para otro ejemplo, considere el circuito básico del amplificador de registro de inversión:
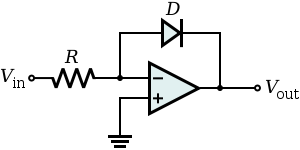
Si resolvemos la ecuación del diodo Shockley
$$ i_D = I_S (e ^ {vD / VT} - 1) $$
para vD, obtenemos $$ v_D = VT \ ln {\ left (\ frac {i_D} {I_S} \ right)} $$ (ignorar el 1, que en su mayoría es irrelevante ya que la exponencial será bastante grande)
Si luego usamos el método corto virtual para ver que $$ i_D = \ frac {v_ {in} - 0} {R_ {in}} $$ obtenemos la expresión correcta para la salida:
$$ v_ {out} = -VT \ cdot \ ln {\ left (\ frac {v_ {in}} {I_S R_ {in}} \ right)} $$
Por lo tanto, el método corto virtual funciona aquí. Pero dado que este diodo será un circuito abierto cuando $$ v_ {out} > v ^ - $$ No estoy seguro de cómo averiguar de antemano que el análisis será válido.