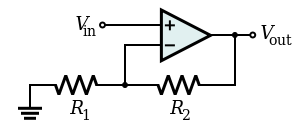
Para derivar esto correctamente de los principios básicos, debe trabajar con la ganancia de bucle abierto del amplificador. Parece que estás confundiendo la ganancia de bucle abierto y bucle cerrado, o tal vez malinterpretando cómo funcionan los amplificadores operacionales. La tensión de salida no es la diferencia entre + y -. Es la diferencia entre + y - multiplicada por la ganancia de bucle abierto.
En las configuraciones de amplificación de amplificadores operacionales, la diferencia entre + y - es siempre muy pequeña. Fracciones de un milivoltio. Es tan pequeño, que podemos entender muchos circuitos con la útil suposición simplificadora de que el voltaje es el mismo en + y -. Esta muy pequeña diferencia de voltaje entre + y - se multiplica por la gran ganancia en bucle abierto para producir la salida. La retroalimentación calibra este diminuto voltaje diferencial para que se obtenga un voltaje de salida razonable a pesar de la enorme ganancia.
Entonces, definamos algunas variables:
$$ A_0 = abierto \ loop \ gain $$
$$ V_ + = voltaje \ en \ + \ terminal $$
$$ V_- = voltaje \ en \ - \ terminal $$
$$ V_ {out} = salida \ voltaje $$
Ahora, tenemos:
$$ V_ {out} = A_o (V_ + - V _-) $$
Pero, dado que tenemos una ruta de retroalimentación, la tensión de salida se establece mediante la tensión de salida mediante el divisor de tensión:
$$ V_- = {R1 \ sobre {R1 + R2}} V_ {out} $$
Para simplificar, reduzcamos esta fracción formada por las resistencias a una sola variable que llamamos f, para retroalimentación:
$$ f = {R1 \ sobre {R1 + R2}} $$
$$ V_- = f V_ {out} $$
Así que ahora podemos sustituir esta V- en la primera fórmula:
$$ V_ {out} = A_o (V_ + - f V_ {out}) $$
El voltaje de salida es el voltaje V +, menos el voltaje de realimentación, escalado por la ganancia de bucle abierto. Tomamos en cuenta el Ao y luego juntamos los términos de Vout:
$$ V_ {out} = A_oV_ + - fA_oV_ {out} $$
$$ V_ {out} + fA_oV_ {out} = A_oV _ + $$
$$ V_ {out} (1 + fA_o) = A_oV _ + $$
$$ V_ {out} = {A_oV _ + \ over 1 + fA_o} $$
Ahora el siguiente paso requiere que hagamos una suposición: la ganancia Ao de bucle abierto del amplificador es muy grande, como 100,000 o más. Lo que esto significa es que el 1 + en la parte inferior no hace ninguna diferencia, porque fAo es un número grande (a menos que f sea un número muy pequeño, pero solo estamos interesados en usar retroalimentación significativa, en lugar de retroalimentación despreciable). Entonces, lo que hacemos es simplemente eliminar el uno:
$$ V_ {out} = {A_oV _ + \ over fA_o} $$
Ahora la ganancia de bucle abierto en la parte superior e inferior se cancela, dejándonos con:
$$ V_ {out} = {V _ + \ over f} $$
La tensión de salida es la tensión de entrada dividida por la realimentación. Si la retroalimentación es 1/5, la tensión de salida es cinco veces la tensión de entrada, etcétera. Ahora un paso más: sustituye la fracción de resistencia por f:
$$ V_ {out} = {V _ + \ sobre {R1 \ sobre {R1 + R2}}} $$
$$ V_ {out} = {{R1 + R2 \ over R1}} V _ + $$
Y por supuesto
$$ {{R1 + R2 \ sobre R1}} = 1 + {R2 \ sobre R1} $$
que es lo que estás buscando.
Nunca olvide que esta sencilla fórmula que relaciona el voltaje de entrada y salida solo funciona porque tanto la retroalimentación como la ganancia de bucle abierto son tan grandes que podemos ignorar el 1 en 1 + fA0. Esta suposición puede romper. Por ejemplo, a frecuencias cada vez más altas, los amplificadores operacionales tienen cada vez menos ganancia de bucle abierto. En alguna frecuencia, la ganancia de bucle abierto se reduce a 1, y luego cae un poco más a frecuencias aún más altas.